1次近似式・2次近似式により,関数の値を1次式や2次式で近似できることを理解する。 1 を発展させて,テイラー多項式及びマクローリン多項式について理解する。 指数・対数・三角関数などについてマクローリン多項式を求めることができる。1次式の計算基礎 文字式では文字の 部分が同じ項 を1つにまとめて式を簡単にすることができる。 例題1 式を簡単にする。 3a 4a 3aと4aは文字の部分がおなじ なのでまとめることができる。 = (3 4)a = 7a 次の式を簡単にせよ。それから何次式になるのか 考えてみましょう。 決して一番前の数字だからといって 決めるわけではありません。 なので、 何次式?と聞かれた場合は、 まず、数字にかけている文字を数えましょう。 次回は 「多項式の次数の数え方」 について説明します。
1
1次式
1次式- 1次不定方程式ax+by=cの一般解を求める手順 1組の整数解x=p,y=qを見つける。 方程式に整数解を代入してa・p+b・q=c(①式)をつくる。 方程式を①式で減算してa(x-p)+b(y-q)=0(②式)をつくる。 1次式への近似 \(n\) 組のデータ \( (x_i \ y_i) \) を回帰式 \( y=abx \) に近似する。 このとき,誤差は \( y_i (a b x_i) \) で表される。 最も確からしい回帰式を与える定数 \(a\),\(b\) は誤差の平方の総和 \( z = \sum \{ y_i (a b x_i) \}^2 \)




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
a=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,1) b=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,2) c=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,3) 多項式(3次式)の近似曲線の式 y=ax^3bx^2cxd 3次式は以下のようになります。 a=INDEX(LINEST(yの範囲, xの範囲^{1,2,3}),1,1) エクセルの1次関数(1次方程式)の計算方法 それでは以下で複数パターンの1次関数(1次方程式)の求め方について確認していきます。 一次方程式(一次関数)のyを求める 今回は例として、y=2x5(-2≦xと≦3で1刻み)いう一次関数の計算を行っていきます。そもそも,条件で示される2つの式 x, x1 と余りを求めたい式 x2 に何の因数も持たないパターンでは,答は定まらないのです.だからそういう問題はないのです. ※3次式が有理係数では因数分解できないが,無理係数,複素係数で因数分解でき,それらの因数が各々与えられた2次式,4次式の
この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。 微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。 部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッとここで、 A 0 = 1 、 k = 1 として A の時間変化を一次反応と二次反応で比較してみると、一次反応では (39) A = e − t となり、二次反応では (310) A = 1 1 2 t となる。 これを同じ t A 平面にプロットすると以下のようになる。 図5.一次反応と二次 中1数学にでてくる1次方程式(xの方程式)の解き方 こんにちは!イボコロリを使ってみたKenだよ。 中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「 1次方程式 」とよばれているものだ。 なにせ、文字が1つしか含まれていないからね。
1 余りによる整数の分類とはどういう意味ですか。 2 コインをn回投げたとき、表が3回連続で出ないような場合の数を$ a_n $とする。 この時の漸化式を教えてください。自然 3 $$ \int_{0}^{π \over 2} cosx \ dx = 1 $$ となるのは何故なんでしょうか? なぜ正(B) また,分母が何次式であっても分母=0のn次方程式は1次式と2次式の積に因数分解することができ (実数解の部分が1次式か重解に,虚数解の2つの組が(2) iii)の形の2次式に対応する) 部分分数分解と恒等式の係数比較法により,上記(1)(2)の形に帰着させる 1つの項に1回ずつ以下ずつ文字がかけられているからね。 じつは、 元:何種類の文字がふくまれているか?? 次:1つの項あたり何回まで文字がかけられているか?? ってことを表しているんだ。 だから、 x y z = 90 っていう方程式は「三元一次方程式



1次发酵 也能做出柔软拉丝的面包 即使放置3天也不硬 绵软十足 考拉海购



头条问答 初中数学一元一次方程有哪些重点 4个回答
1次式と2次式の使用例を示します。 例1: 単価100円の品物をx個買った金額は、100x という 1次式 で表せます。 千円札を出してお釣りが0円の場合、何個買ったでしょうか。 一次式の項とまとめ方の復習 基本一次式の項とまとめ方 で見た、一次式の項のまとめ方について振り返っておきましょう。 2x −3x 2 x − 3 x という式について考えます。 式の中で、 で区切られているものを、 項 というのでした。 今の場合、 2x (−3x) 2 x ( − 3 x) と書けるので、項は、 2x 2 x, −3x − 3 x の2つとなります。 どちらも x x を1つだけ含んでい 次の多項式は何次式か。 (1)ax+by+cz (2)ax2乗+3bxy-cy2乗 次の式を簡単にせよ。 (1)2分の3x+2y-4分の5x-y 数学の宿題の問題です。 教科書見てもわかんなくて、出すたびに再提出になっています>< よかったら、解説もお願い致します。




几次几项式怎么判断 百度经验
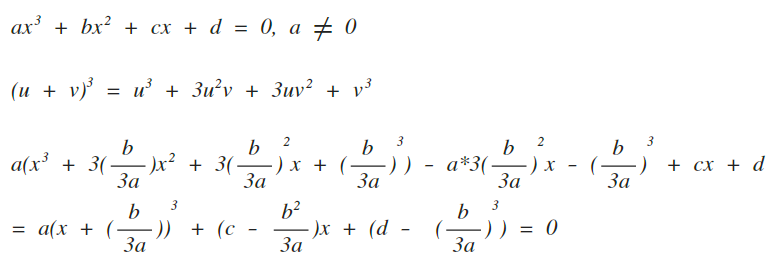



高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium
まずはデータの図示 フィッティンブカーブを描く x 座標を作る Numpypolyfit を用いた最小二乗法 Sympy を用いた数式の表示の準備 最小二乗法によるカーブフィッティング(1次式から9次式まで) 参考1次式と数の除法 項が1つの1次式と数の除法 係数と数を計算してから文字をかける 例24x ÷ 8 = 24 ÷ 8 × x ← 係数を数でわる = 3x 確認計算しなさい 答表示 8x÷4 2x18x ÷ (9) 2x 15x ÷ (6)5 2 x 項が2つの1次式と数の除法 項が複数の式と数の除法は 分配文字の項で、文字にかけてある数の部分を 係数 かけあわされている文字の個数を、その式の 次数 といいます。 また、 次数が2 の式を 2次式 といいます。 同様に次数が3であれば3次式、4であれば4次式というように その式が何次式であるかを判断します。 つまり、式の次数を調べれば何次式になるかがわかるということです。 それでは、次の単項式の係数、次数




Hario ハリオ V60 1次抽取式滤杯mugen 咖啡滤杯1 2杯用白色日本制造vdmu 02 Cw 亚马逊中国 家居生活



小学方程
N=1のとき1次式、n=2のとき2次式になります。それぞれ下記に示します。 x1 x 2 1 また次数が1の場合は、x 1 と書きません。xのままでOKです。1次式、2次式の詳細は下記をご覧ください。 1次式と変形できるのは 1次式だけではありません 。 ただ、ここでは1次式だけの処理のしかたを説明しておきました。 よく見る形ですしね。 係数比較は定数のときもありましたよね。 覚えていないかもしれないけど、強引に係数比較か?特性方程式か?って。11 不定積分 年10 月 日 有理式の定石に則って、分母を因数分解する。 I3 = Z 1 (x 1)(x2 − x 1)dx (15) 部分分数分解をして I3 = 1 3 Z 1 x 1 − x − 2 x2 − x 1 dx = 1 3 lnx 1− 1 3 Z x − 1 2




正定二次型和正定矩阵 黎明晨光
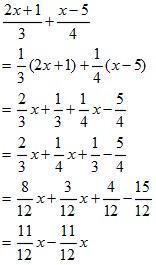



Math 1次式の計算 分数式の計算の指導法を考える 働きアリ
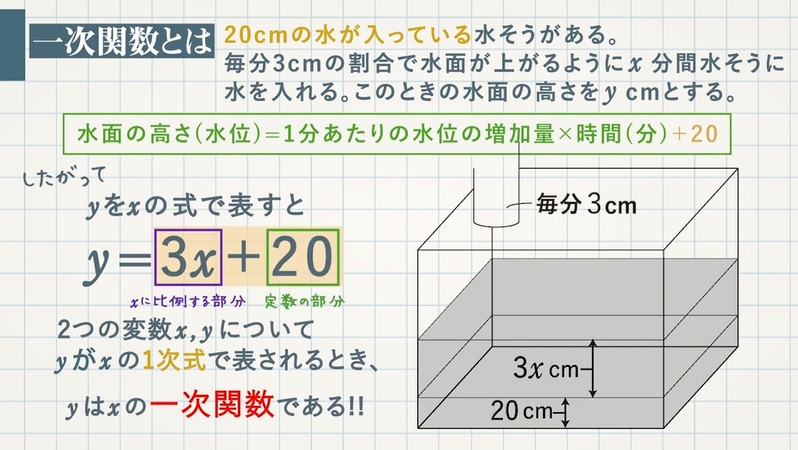
1次関数とは yをxの1次式で表せる関数のことである。 1次関数の式 y=axb a,bは定数 確認 次の中から1次関数をすべて選べ。 y = 5x 2 y = 3x 2 y= x 2 y = 3 x 12x2y4=0 ①③⑤ ②は2次関数、③はa= 1 2 , b=0の1次関数、④は反比例、⑤は変形するとy=6x2となる。 整式 P ( x) P ( x) を 1 1 次式 x − k x − k で割った余りは、 P ( k) P ( k) に等しい。 またまたさっきの例題に、今突如として出てきた剰余の定理を用いてみましょう。 今回、 x − 2 x − 2 で割っているので、 P ( x) = x 3 − x 2 x − 1 P ( x) = x 3 − x 2 x − 1 に x = 2 x = 2 を代入してみましょう。 すると、 P ( 2) = 2 3 − 2 2 2 − 1 = 8 − 4 2 − 1 = 5 P ( 2) = 2 3 − 2 2 2 − 1 = 8 −= dt= tan −1 tC= tan −1 (x1)C (3) この形に当てはまると非常に簡単に不定積分が得られるので,上記(1)~(2) i)iii)に当てはまるか否かによらず f'(x)/f(x) 形でないかどうか瞬間チェックするとよい




ベストオブ一次方程式問題集 ぬりえ壁紙hd



尴尬 台湾汉光兵推台军过去仅赢1次 今年改成综合式研讨没有胜负 大陆
多項式の用語 式 2x-5 を 多項式 といい、2x と-5 の2つの 項 からできています。 x の前の数 2 を 係数 といいます。 また、項 2x=2x 1 の次数は 1 次で、項 -5=-5x 0 は0次なので、この多項式は 1次式 です(最大の次数で表します)。 多項式 2x 2 -3x+4 は、2x 2 と-3x と4 の3つの項からできています。 x 2 の係数は2、 x の係数は-3です。 各項の次数は、2x 2 は2次1次反応の見分け方 反応次数の求め方 ただ、0次反応ではなく、1次反応、2次反応と次数が増えると、濃度変化は一定でなくなります。それでは、どのようにこれらの化学反応の反応次数を見分けるといいのでしょうか? 以下で確認していきます。例 1 多項式 P(x)=x 2 x3 を1次式 x−1 で割る計算は右のようになるが、このときの余りは P(x) の x に 1 を代入するだけで求めることができる。 P(1)=1 2 13=5 2 多項式 P(x)=x 2 −3x4 を1次式 x2 で割る計算は右のようになるが、このときの余りは P(x) の x に −2 を代入するだけで求めること




因式分解技巧 二元二次的分解 星空暗流 博客园



与式が 1次式の積となるようにするとき Kの値を求めよ という問 Yahoo 知恵袋
1次式どうしの乗法 次に(a2)(b1)のように1次式どうしの掛け算を展開する。 この場合も 分配法則 を使う。 (例) (a2)(b1)を展開する場合 (a 2) (b 1) このようにaをbと1の両方に、2をbと1の両方にそれぞれ掛ける。 (a2)(b1) = aba2b2 展開の基本は分配法則である。方程式の解き方基本1 まずは x を含む項を左辺に集め、数字だけの項は左辺から消してしまいましょう! 基本1)左辺を x のエリア、右辺を数字のエリアと考えます。 基本2)左辺を x だけにしたいので、じゃまな「+3」を無くすために「-3」をし 各項の最大次数は1なので、上の式を1次式と呼びます。 では、1次式のグラフを見てみましょう。 \( y = ax b(a > 0 )\)のグラフ




洛杉矶仁美整形医美 童颜针8折 购3d脸部提拉术送全脸美版超声刀1次 拥有水光针 瘦脸针 高端韩式皮肤管理等专业整形美容项目 北美省钱快报




浅谈有理分式的拆解技巧 真假都有 哔哩哔哩
1次式の計算のしかた (1) 文字の項どうし,数の項どうしをまとめて簡単にします. 文字の項と数字の項とで係数は完全に分けて計算します.これらが混ざることはありません.集合 a の各要素を集合 b の要素に対応させる規則を a から b への写像という. 写像のうち特に元の集合と対応させる集合とが同一であるものを変換という.(ある集合 a から集合 a 自身への写像) ここでは,さらに限定して変換のうちで対応の規則が「定数項のない1次式」で表される1次変換1次関数の表し方とは? yがxの 1次式 で表されるとき、 yはxの1次関数である と教科書では説明されます。 教科書だけでは ピンとこないかもしれませんが、 要するに、 y = ax + b という形になったら1次関数です。 このように覚えるのが、




1 3多項式的乘除運算乙




Ppt 4 1 因式分解解一元二次方程式powerpoint Presentation Id




人教版数学 七年级下册第八章 消元 解二元一次方程组 三好网



一元二次方程式




中学1年生 数学 無料問題集 一次式と数の乗法 掛け算 おかわりドリル




一元一次方程知識講解 經典例題講解 每日頭條




項 係数 一次式とは 中1数学 Youtube




第一次世界大战期间 各国装备的枪械 都有哪些特征 快资讯




90后女孩不结婚 不社交 1年只剪1次头 3年怒攒一套别墅 凤凰网




C一元一次方程12 Pdf




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Sp骁浪荒川之主技能削弱 一觉起来浪 了 削弱 伤害 生命上限30 不会再 来自网易大神阴阳师圈子 飞星飘雪




行列式负一次方 行列式中负一的几次方是怎么回事啊 求大佬带 三人行教育网 Www 3rxing Org




スタディピア 1次方程式




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一般 一元一次式的化簡 分數型1 Youtube




一元一次式和一元一次方程式哪裡不一樣 數學 均一教育平台




觀念 一元一次方程式的意義 數學 均一教育平台




高中生到熟女都在問一元三 四次方程式怎麼解 註 Medium目前不支援latex 雖然我也不太會用 By Thomas Anderson Medium



一次関数とは Yがxの1次式で表される関数 教遊者



牛頓一次因式檢驗法 X的創作 巴哈姆特




一般 解一元一次方程式 等式兩邊未知數的比較 已下架內容 均一教育平台




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




朗斯基行列式 搜狗百科




1 次方程式問題 シモネタ




正则表达式匹配0次1次或者无限次 Py编程 爱分享o0 希恩 Csdn博客 Python正则表达式中 匹配其前导元素0次或1次




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




多出来的孩子 Sqr5 S Blog




分布式系统接口幂等性 Segmentfault 思否




二元一次方程组的解法 知乎




一次関数とは Yがxの1次式で表される関数 教遊者




1次式の加減法 カッコの前にマイナスがある時は解き方に注意 中学や高校の数学の計算問題




基礎 多項式的除法 二次式除以一次式 已下架內容 均一教育平台



1




01一元一次方程的概念一元一次方程初中数学初一 Youtube




一元一次方程高频考点 经典题型演练 楠木轩




一元二次方程配方法 4道提高题 雪花新闻




ユニーク中学1 年数学方程式 ぬりえ壁紙hd
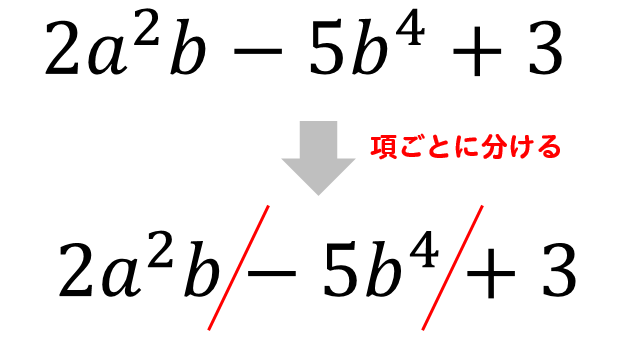



単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ



一次方程 维基百科 自由的百科全书




滿千免運 11 17 現貨哩亞ilia Max 10口一次性能量棒拋棄式 露天拍賣



一元一次方程式及其解 七上第三章一元一次方程式 發現學習的美麗新世界




如何求部分分式 部分分式分解求过程 三人行教育网 Www 3rxing Org




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



高校数学 2元2次式が1次式の積に因数分解できるための条件 受験の月




习近平的8月



Ycvs Ntpc Edu Tw




中1 一次式 項 係数 まとめ 中学生 数学のノート Clearnote



代數之一元一次式 Live 多媒體數學觀念典online




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく



二元二次多项式的因式分解 一 哔哩哔哩 Bilibili



式神强度调整平民战神sp荒川被大削 阴阳师 阴阳师手游专区 Com 中国游戏第一门户站



1




最も共有された 1 次方程式分数 シモネタ




画像をダウンロード中1 数学文字式加法減法 シモネタ




最も共有された 1 次方程式分数 シモネタ



3的n次方减3的n 1次方等于多少3的n次方减3的n 1次方等于多少 天奇生活



天天快报




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



因式分解法解一元二次方程 禾教 初中数学互动课堂




Ppt 第十二章曲线回归powerpoint Presentation Free Download Id




几次几项式怎么判断 百度经验




一元二次方程根与系数的关系



1次方 1次方怎么算



3元1次方程的解法daan 关于3元1次方程组的解法答案



初中数学 一元二次方程 这些题不会做 你怎好意思说学懂了配方法 高中数学爱做初中数学题 微信公众号文章阅读




Wel鲸鱼轻烟pro电子烟套装 1烟杆 2烟弹 水果味蒸汽烟新款便携充电式一次性雾化换弹小烟戒烟1灰色机身 雾化弹2 图片价格品牌报价 京东




Matlab数学实验第七章符号计算 Ppt Download



漸化式 Nの1次式が付いてるタイプ 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ




数学1年



韦达定理 一元二次方程根与系数的关系 新华网



1次関係式




齐次方程的 齐次 代表什么 知乎




洛杉矶仁美整形医美 童颜针8折 购3d脸部提拉术送全脸美版超声刀1次 拥有水光针 瘦脸针 高端韩式皮肤管理等专业整形美容项目 北美省钱快报




次数の意味から5分でわかる 一次式と二次式の違い Qikeru 学びを楽しくわかりやすく




高校数学 置換積分の一種 1次式置換型 置換せずに瞬殺せよ 受験の月




二元一次方程式的意義與列式 Youtube




圖一 除式次數變少時 餘式要繼續除完 Clearnote




絶対値を含む方程式 不等式 基本編 1次式 おいしい数学




沉浸式文旅 剧本杀能否创造新风口




一元二次方程配方法 4道提高题 雪花新闻




この式は一次式ですか それとも一次式ではありませんか Clearnote



名師課輔網 一次因式檢驗法




有名な中一数学方程式 ぬりえ壁紙hd



有利関数の積分で1次式 1次式2次式 2次式の計算方法教えてください2 Yahoo 知恵袋




二元一次式二元一次式的化簡二元一次方程式自我評量 Ppt Download




北京大学 高等代数 第一章代数学的经典课题 1 2 一元高次代数方程的基础知识 小库档文库




第十一章曲线回归第一节曲线的类型与特点第二节曲线方程的配置第三节多项式回归 Ppt Download




中学1年生 数学 文字と式 一次式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



连续两年丨sparrow流式细胞仪满分通过21全国流式细胞仪术室间质量评价 赛雷纳 中国 医疗科技有限公司



0 件のコメント:
コメントを投稿